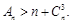(本小题满分10分)
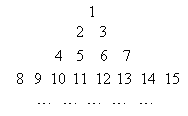
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第 行共有
行共有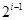 个正整数,设
个正整数,设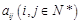 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第 行,从左往右第
行,从左往右第 个数.
个数.
(1)求 的值;
的值;
(2)用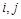 表示
表示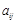 ;
;
(3)记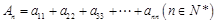 ,求证:当
,求证:当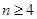 时,
时,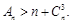
推荐套卷
(本小题满分10分)
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第 行共有
行共有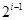 个正整数,设
个正整数,设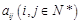 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第 行,从左往右第
行,从左往右第 个数.
个数.
(1)求 的值;
的值;
(2)用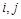 表示
表示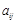 ;
;
(3)记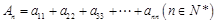 ,求证:当
,求证:当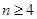 时,
时,