(14分)如图,抛物线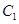 :y=ax2+bx+1的顶点坐标为D(1,0),
:y=ax2+bx+1的顶点坐标为D(1,0),
(1)求抛物线
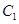 的解析式;
的解析式;(2)如图1,将抛物线
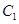 向右平移1个单位,向下平移1个单位得到抛物线
向右平移1个单位,向下平移1个单位得到抛物线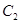 ,直线
,直线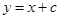 ,
,
经过点D交y轴于点A,交抛物线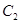 于点B,抛物线
于点B,抛物线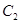 的顶点为P,求△DBP的面积;
的顶点为P,求△DBP的面积; 如图2,连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
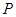 至点
至点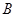 之间的一动点,
之间的一动点,
连结 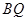 并延长交
并延长交 于点
于点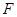 ,试问:当点Q运动到什么位置时,△BCF的面积为
,试问:当点Q运动到什么位置时,△BCF的面积为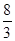 。
。
相关知识点
推荐套卷
(14分)如图,抛物线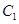 :y=ax2+bx+1的顶点坐标为D(1,0),
:y=ax2+bx+1的顶点坐标为D(1,0),
(1)求抛物线
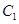 的解析式;
的解析式;(2)如图1,将抛物线
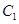 向右平移1个单位,向下平移1个单位得到抛物线
向右平移1个单位,向下平移1个单位得到抛物线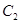 ,直线
,直线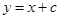 ,
,
经过点D交y轴于点A,交抛物线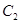 于点B,抛物线
于点B,抛物线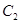 的顶点为P,求△DBP的面积;
的顶点为P,求△DBP的面积; 如图2,连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
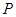 至点
至点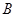 之间的一动点,
之间的一动点,
连结 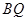 并延长交
并延长交 于点
于点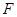 ,试问:当点Q运动到什么位置时,△BCF的面积为
,试问:当点Q运动到什么位置时,△BCF的面积为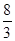 。
。