．（本小题满分13分）
P为椭圆
上任意一点，
为左、右焦点，
如图所示．
(1)若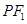
的中点为
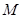，求证: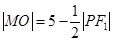
(2)若∠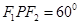
，求|PF1|·|PF2|之值；
(3)椭圆上是否存在点P，使·＝0，若存在，求出P点的坐标，若不存在，试说明理由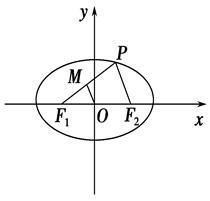
相关试题
，
，且
，求
的值。
，求：
；
的最小值是
，
求实数
的值。
表示什么曲线？（其中
是常数，且
为正数，
为变量。）
为圆
：
上任意一点，且
为原点，
，求
的取值范围
。
，
，且
。
的表达式化为
的形式；
，求函数
与
的夹角为
，若
，
，试求
与
的夹角
。推荐套卷
．（本小题满分13分）
P为椭圆上任意一点，为左、右焦点，如图所示．
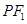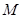(1)若的中点为，求证: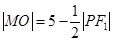
(2)若∠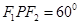，求|PF1|·|PF2|之值；
(3)椭圆上是否存在点P，使·＝0，若存在，求出P点的坐标，若不存在，试说明理由
粤公网安备 44130202000953号