小明到某品牌服装专卖店做社会调查.了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,而“计件奖金=销售每件的奖金×月销售件数”,并获得如下信息:
| 营业员 |
甲 |
乙 |
| 月销售件数(件) |
200 |
150 |
| 月总收入(元) |
1400 |
1250 |
列方程(组),求营业员的月基本工资和销售每件的奖金;
营业员丙月总收入不低于
 元,这位营业员当月至少要卖服装多少件?
元,这位营业员当月至少要卖服装多少件?
相关知识点
推荐套卷
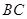 是以线段
是以线段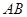 为直径的
为直径的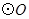 的切线,
的切线,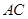 交
交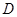 ,过点
,过点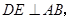 垂足为点
垂足为点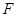 ,连接
,连接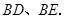
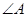 =
=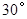 ,
,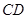 =
=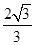 ,求
,求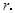
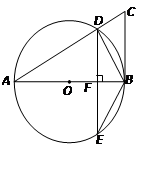
 粤公网安备 44130202000953号
粤公网安备 44130202000953号