已知函数 .
.
(Ⅰ)化简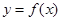 的表达式并求函数的周期;
的表达式并求函数的周期;
(Ⅱ)当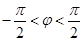 时,若函数
时,若函数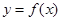 在
在 时取得最大值,求
时取得最大值,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,将函数 图象上各点的横坐标扩大到原来的
图象上各点的横坐标扩大到原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数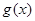 的图象,求函数
的图象,求函数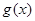 的单调递增区间.
的单调递增区间.
相关知识点
推荐套卷
已知函数 .
.
(Ⅰ)化简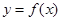 的表达式并求函数的周期;
的表达式并求函数的周期;
(Ⅱ)当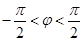 时,若函数
时,若函数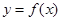 在
在 时取得最大值,求
时取得最大值,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,将函数 图象上各点的横坐标扩大到原来的
图象上各点的横坐标扩大到原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数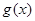 的图象,求函数
的图象,求函数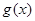 的单调递增区间.
的单调递增区间.