(本题满分6分)
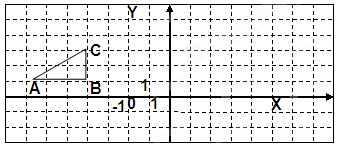
如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，Rt△ABC的顶点均在格点上，在
建立平面直角坐标系以后，点A的坐标为（-6，1），点B的坐标为（-3，1）,点C的坐标为（-3，3）．（1）将Rt△ABC沿X轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出Rt△A1B1C1的图形，并写出点A1的坐标。
（2）将原来的Rt△ABC绕着点B顺时针旋转90°得到Rt△A2B2C2，试在图画出Rt△A2B2C2的图形。
如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数
（x＞0）图象上，△BOC的面积为8．
（1）求反比例函数
的关系
（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？
（3）当运动时间为
秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
如图，直线
的解析表达式为
，且与
轴交于点
，直线
经过点
，直线，交于点
．
（1）求点的坐标；
（2）求直线的解析表达式；
（3）求
的面积；（4）在直线上存在异于点的另一点
，使得
与的面积相等，请直接写出点的坐标．
如图，四边形ABCD为正方形，点A的坐标为（0，2），点B的坐标为（0，-3），反比例函数
的图象经过点C，一次函数y=ax+b的图象经过点A.C
（1）求反比例函数和一次函数的解析式
（2）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，请直接写出P点的坐标.
一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，
结合图象回答下列问题：（1）农民自带的零钱是多少？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
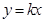的图象与反比例函数
（
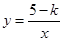为常数，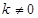
）的图象有一个交点的横坐标是2．
，
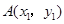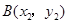是反比例函数
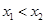，试比较
的大小．
粤公网安备 44130202000953号