.(14分)已知椭圆
＋
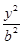＝1(a>b>0)的左、右焦点分别是F1(－c,0)，F2(c,0)，Q是椭圆外的动点，满足
＝2a.点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足
，
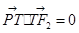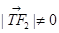
(1)设x为点P的横坐标，证明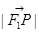
＝a＋
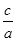x；
(2)求点T的轨迹C的方程；
(3)试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S＝b2？若存在，求∠F1MF2的正切值；若不存在，请说明理由．
相关试题
的定义域为
，函数
的定义域为
.
，求实数
的取值范围.
的顶点
.
为坐标原点.
的外接圆
的方程；
作圆的切线
，设
轴、
轴的正半轴分别
、
，求
面积的最小值.
与直角梯形
所在平面互相垂直，
，
，
.
平面
；
平面
；
的体积.
：
与直线
：
平行,求实数
的值；
：
与
：
的交点
且垂直于直线
：
直线方程.
，g(x)＝alnx，a∈R.推荐套卷
.(14分)已知椭圆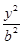＋＝1(a>b>0)的左、右焦点分别是F1(－c,0)，F2(c,0)，Q是椭圆外的动点，满足＝2a.点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足，
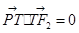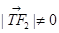
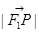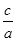(1)设x为点P的横坐标，证明＝a＋x；
(2)求点T的轨迹C的方程；
(3)试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S＝b2？若存在，求∠F1MF2的正切值；若不存在，请说明理由．
粤公网安备 44130202000953号