(本小题满分12分).如图,在直角梯形 中,
中,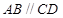 ,
, ,且
,且 ,现以
,现以 为一边向形外作正方形
为一边向形外作正方形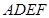 ,然后沿边
,然后沿边 将正方形
将正方形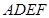 翻折,使平面
翻折,使平面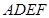 与平面
与平面 垂直,
垂直, 为
为 的中点
的中点
(I) 求证: 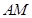 ∥平面
∥平面 ;
;
(Ⅱ)求证: 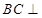 平面
平面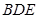 ;
;
(III) 求二面角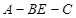 的大小.
的大小.
推荐套卷
(本小题满分12分).如图,在直角梯形 中,
中,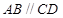 ,
, ,且
,且 ,现以
,现以 为一边向形外作正方形
为一边向形外作正方形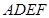 ,然后沿边
,然后沿边 将正方形
将正方形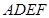 翻折,使平面
翻折,使平面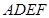 与平面
与平面 垂直,
垂直, 为
为 的中点
的中点
(I) 求证: 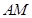 ∥平面
∥平面 ;
;
(Ⅱ)求证: 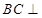 平面
平面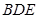 ;
;
(III) 求二面角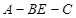 的大小.
的大小.