有研究发现,人体 在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下
在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下 表:
表: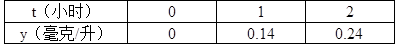
(1)求y与t的函数关系式;
(2)在注射后的第几小时,该病人体内的血药浓度达到最大?最大浓度是多少?
(3)该病人在注射后的几个小时内,体内的血药浓度超过0.3毫克/升?
相关知识点
推荐套卷
有研究发现,人体 在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下
在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如下 表:
表: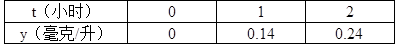
(1)求y与t的函数关系式;
(2)在注射后的第几小时,该病人体内的血药浓度达到最大?最大浓度是多少?
(3)该病人在注射后的几个小时内,体内的血药浓度超过0.3毫克/升?