△ABC的三个角A,B,C所对的边分别是a,b,c,向量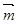 =(2,-1),
=(2,-1),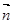 =(sinBsinC,
=(sinBsinC,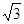 +2cosBcosC),且
+2cosBcosC),且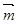 ⊥
⊥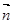 。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(
。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(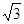 +1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△
+1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△ ABC的面积。
ABC的面积。
相关知识点
推荐套卷
△ABC的三个角A,B,C所对的边分别是a,b,c,向量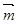 =(2,-1),
=(2,-1),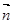 =(sinBsinC,
=(sinBsinC,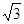 +2cosBcosC),且
+2cosBcosC),且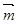 ⊥
⊥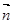 。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(
。⑴求角A的大小。⑵现给出以下三个条件:①B=45º;②2sinC-(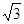 +1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△
+1)sinB=0;③a=2。试从中再选择两个条件以确定△ABC,并求出所确定的△ ABC的面积。
ABC的面积。