已知双曲线方程为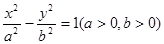
，椭圆C以该双曲线的焦点为顶点，顶点为焦点。
（1）当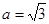
，
时，求椭圆C的方程；
（2）在（1）的条件下，直线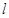
：
与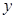
轴交于点P，与椭圆交与A，B两点，若O为坐标原点，
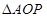与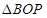
面积之比为2：1，求直线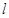的方程；
（3）若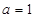
，椭圆C与直线
：
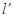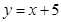有公共点，求该椭圆的长轴长的最小值。
相关试题
.设方程
的系数
和
分别是先后抛掷一枚骰子得到的点数．
，当
时，其前
项和
满足
；
，求数列｛
｝的前项和
有相同的焦点，且椭圆过点
，
过点
交椭圆于
两点，且
，求直线
中，
∠
=90°，
，
⊥
.
（Ⅰ）求证：
；
的体积.
中，已知
，
，
．
（1）求
的值；（2）求
的值．相关知识点
推荐套卷
已知双曲线方程为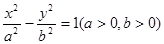，椭圆C以该双曲线的焦点为顶点，顶点为焦点。
（1）当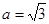，时，求椭圆C的方程；
（2）在（1）的条件下，直线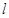：与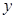轴交于点P，与椭圆交与A，B两点，若O为坐标原点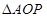，与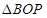面积之比为2：1，求直线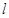的方程；
（3）若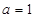，椭圆C与直线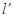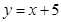：有公共点，求该椭圆的长轴长的最小值。
粤公网安备 44130202000953号