在如图所示的空间几何体中，平面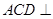
平面ABC，
AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在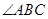
的平分线上。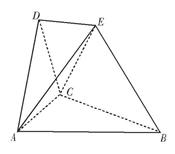
（1）求证：DE//平面ABC；
（2）求二面角E—BC—A的余弦值；
，求
的其他三角函数值．
，集合
，求
．
，
，求证：
．
随时间
变化的函数为
．
时的电流强度．
，
：
经过怎样的变换，得到该函数的图象．推荐套卷
在如图所示的空间几何体中，平面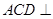平面ABC，
AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在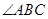的平分线上。
（1）求证：DE//平面ABC；
（2）求二面角E—BC—A的余弦值；
粤公网安备 44130202000953号