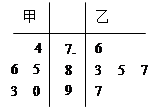甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
（1）现要从中选派一人参加英语口语竞赛，从统计学角度，你认为派哪位学生参加更合适，请说明理由；
（2）若将频率视为概率，对学生甲在今后的三次英语口语竞赛成绩进行预测，记这三次成绩中高于80分的次数为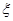
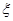，求的分布列及数学期望
.
相关试题
的图像过点
，点
关于直线
的对称点
在
的图像上。
，求
的最小值及取得最小值时
的值。
的单调性；
上是增函数，求
的取值范围。
中，
的中点，
上一点，且
时，求证：
;
与平面
所成的角为
，求
的值。
的图像关于直线
对称，且图像上相邻两个最高点的距离为
。
和
的值；
，求
的值。
中，
是
中点．
⊥平面
；
，求二面角
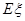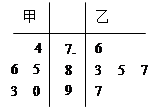
的大小．推荐套卷
甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
（1）现要从中选派一人参加英语口语竞赛，从统计学角度，你认为派哪位学生参加更合适，请说明理由；
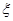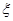（2）若将频率视为概率，对学生甲在今后的三次英语口语竞赛成绩进行预测，记这三次成绩中高于80分的次数为，求的分布列及数学期望.
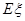粤公网安备 44130202000953号