已知等比数列 的首项
的首项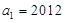 ,公比
,公比 ,数列
,数列 前n项和记为
前n项和记为 ,前n
,前n
项积记为 .
.
(Ⅰ)求数列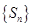 的最大项和最小项;
的最大项和最小项;
(Ⅱ)判断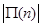 与
与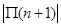 的大小, 并求
的大小, 并求 为何值时,
为何值时, 取得最大值;
取得最大值;
(Ⅲ)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
些等差数列的公差按从小到大的顺序依次设为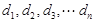 ,证明:数列
,证明:数列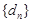 为等比数列。
为等比数列。
(参考数据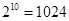 )
)
相关知识点
推荐套卷
已知等比数列 的首项
的首项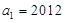 ,公比
,公比 ,数列
,数列 前n项和记为
前n项和记为 ,前n
,前n
项积记为 .
.
(Ⅰ)求数列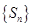 的最大项和最小项;
的最大项和最小项;
(Ⅱ)判断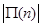 与
与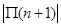 的大小, 并求
的大小, 并求 为何值时,
为何值时, 取得最大值;
取得最大值;
(Ⅲ)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这
些等差数列的公差按从小到大的顺序依次设为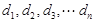 ,证明:数列
,证明:数列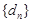 为等比数列。
为等比数列。
(参考数据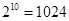 )
)