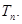（本小题满分14分）
已知函数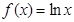
的图象是曲线C，点
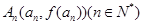是曲线C上的一系列点，
曲线C在点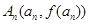
处的切线与y轴交于点
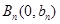。若数列
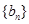是公差为2的等差
数列，且
（1）分别求出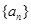数列
与数列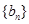的通项公式；
（2）设O为坐标原点，
表示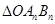
的面积，求数列
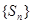的前项n和
，求证：
不可能都是奇数。
若非
是
的
充分不必要条件，求
的取值范围。
”的逆命题、否命题、逆否命题，并判断它们的真假.
中，以O为圆心的圆与直线
相切.
轴相交于
两点，圆内的动点
满足
，求
的取值范围.
已知
的最大值和最小
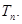
值.推荐套卷
（本小题满分14分）
已知函数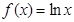的图象是曲线C，点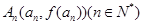是曲线C上的一系列点，
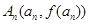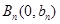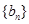曲线C在点处的切线与y轴交于点。若数列是公差为2的等差
数列，且
（1）分别求出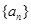数列与数列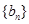的通项公式；
（2）设O为坐标原点，表示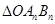的面积，求数列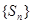的前项n和
粤公网安备 44130202000953号