抛掷A,B,C三枚质地不均匀的纪念币，它们正面向上的概率如下表所示
；
| 纪念币 |
A |
B |
C |
| 概率 |
 |
a |
a |
将这三枚纪念币同时抛掷一次，设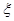
表示出现正面向上的纪念币的个数。
（1）求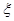的分布列及数学期
望；
（2）在概率
中，若
的值最大，求a的最大值。
相关试题
是等差数列，
是各项都为正数的等比数列，且
，
，
。
的前n项和
。
满足
，
是等比数列；
中，
前
项和为
，且点
在直线
上，
的值。
中，内角
对边的边长分别是
，已知
，
。
的面积等于
，求
。
，求推荐套卷
抛掷A,B,C三枚质地不均匀的纪念币，它们正面向上的概率如下表所示；
| 纪念币 |
A |
B |
C |
| 概率 |
|
a |
a |
将这三枚纪念币同时抛掷一次，设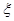表示出现正面向上的纪念币的个数。
（1）求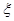的分布列及数学期望；
（2）在概率中，若的值最大，求a的最大值。
粤公网安备 44130202000953号