（本小题满分12分）已知矩形ABCD的边长
,一块直角三角板
PBD的边
，且
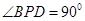，如图．
（1）要使直角三角板PBD能与平面ABCD垂直放置，求
的长；
（2）在（1）的条件下，求二面角
的平面角的余弦值．
的最小值.
，且与直线2x-y+4=0的交点在x轴上的直线的方程。
的直线的方程.相关知识点
推荐套卷
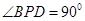（本小题满分12分）已知矩形ABCD的边长,一块直角三角板PBD的边，且，如图．
（1）要使直角三角板PBD能与平面ABCD垂直放置，求的长；
（2）在（1）的条件下，求二面角的平面角的余弦值．
粤公网安备 44130202000953号