如图，在直角梯形ABCD中，AB∥DC，∠D=90o，AC⊥BC，AB=10cm,BC=6cm，F点以2cm／秒的速度在线段AB上由A向B匀速运动，E点同时以1cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒(0<t<5)．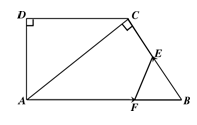
（1）求证：△ACD∽△BAC；
（2）求DC的长；
（3）设四边形AFEC的面积为y，求y关于t的函数关系式，并求出y的最小值．
相关试题
．
，求作△ABC，使得BC = a，AC = b，
．（不写作法，保留作图痕迹）．
；
；
……
相关知识点
推荐套卷
如图，在直角梯形ABCD中，AB∥DC，∠D=90o，AC⊥BC，AB=10cm,BC=6cm，F点以2cm／秒的速度在线段AB上由A向B匀速运动，E点同时以1cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒(0<t<5)． （1）求证：△ACD∽△BAC；
（2）求DC的长；
（3）设四边形AFEC的面积为y，求y关于t的函数关系式，并求出y的最小值．
粤公网安备 44130202000953号