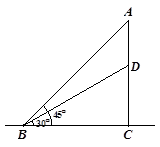
响应“绿色环保,畅通出行”的号召,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍增加,已知原楼梯BD长20米,在楼梯水平长度(BC)不发生改变的前提下,楼梯的倾斜角由30°增大到45°,
那么新修建的楼梯高度将会增加多少米?
(结果保留整数,参考数据: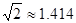 ,
,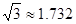 )
)
相关知识点
推荐套卷
响应“绿色环保,畅通出行”的号召,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍增加,已知原楼梯BD长20米,在楼梯水平长度(BC)不发生改变的前提下,楼梯的倾斜角由30°增大到45°,
那么新修建的楼梯高度将会增加多少米?
(结果保留整数,参考数据: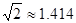 ,
,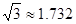 )
)