(本题满分10分)
已知抛物线
上横坐标为
的点
到焦点
的距离为
．
（I）求抛物线的方程；
（II）若斜率为
的直线
与抛物线
交于
两点，且点
在直线的右上方，求证：△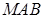
的内心在直线
上；
（III）在（II）中，若
，求
的内切圆半径长．
相关试题
，曲线
在点
处的切线平行于直线
,若函数
在
时有极值．
,
的值；
的单调区间； 
上的的最大值为10，求
满足
的解析式；
在区间
上是减函数，求非负实数
的取值范围。
与
的图像都过
，且在点P处有相同的切线．
的值；
，求
的单调区间．
与
是函数
的两个极值点．
和
的值；
的极大值还是极小值，并说明理由．
是定义在R上的奇函数，当
时，
。
时，
的解析式；推荐套卷
(本题满分10分)
已知抛物线上横坐标为的点到焦点的距离为．
（I）求抛物线的方程；
（II）若斜率为的直线与抛物线交于两点，且点在直线的右上方，求证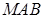：△的内心在直线上；
（III）在（II）中，若，求的内切圆半径长．
粤公网安备 44130202000953号