投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是 ,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域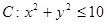 上的概率;
上的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
推荐套卷
投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是 ,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域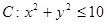 上的概率;
上的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.