如图，已知正方形ABCD在直线MN的上方，边BC在直线MN上，E是线段BC上一点，以AE为边在直线MN的上方作正方形AEFG，其中AE=2，记∠FEN=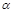
，△EFC的面积为S.
(1)求S与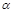之间的函数关系；
(2)当角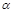取何值时S最大？并求S的最大值。
相关试题
，数列
满足条件：
．
为等比数列；
令
是数
列
的前
项和，求使
成立的最
小的
.
的单调区间；
恒成立，求实数a的取值范围．
13分)设等差数列
满足
.
.
，且
为第一象限角，求y的值；
，求y的值．
在定义域
上是减函数，满足f(1-a)+f(1-
2a)〈0，求
的取值范围。推荐套卷
如图，已知正方形ABCD在直线MN的上方，边BC在直线MN上，E是线段BC上一点，以AE为边在直线MN的上方作正方形AEFG，其中AE=2，记∠FEN=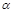，△EFC的面积为S.
(1)求S与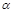之间的函数关系；
(2)当角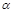取何值时S最大？并求S的最大值。
粤公网安备 44130202000953号