.已知抛物线 的准线为
的准线为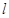 ,焦点为F,
,焦点为F,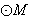 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与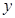 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为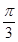 的直线
的直线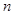 ,交
,交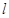 于点A,交
于点A,交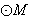 于另一点B,且AO=OB=2.
于另一点B,且AO=OB=2.
(1)求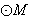 和抛物线C的方程;
和抛物线C的方程;
(2)若P为抛物线C上的动点,求 的最小值;
的最小值;
(3)过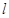 上的动点Q向
上的动点Q向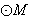 作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
推荐套卷
.已知抛物线 的准线为
的准线为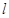 ,焦点为F,
,焦点为F,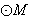 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与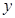 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为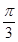 的直线
的直线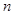 ,交
,交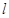 于点A,交
于点A,交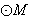 于另一点B,且AO=OB=2.
于另一点B,且AO=OB=2.
(1)求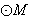 和抛物线C的方程;
和抛物线C的方程;
(2)若P为抛物线C上的动点,求 的最小值;
的最小值;
(3)过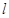 上的动点Q向
上的动点Q向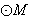 作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.