（本小题满分12分）将编号为1，2，3，4的四张同样材质的卡片，随机放入编码分别为1，2，3，4的四个小盒中，每盒仅放一张卡片，若第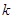
号卡片恰好落入第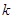号小盒中，则称其为一个匹对，用
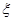表示匹对的个数.
（1）求第2号卡片恰好落入第2号小盒内的概率;
（2）求匹对数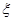的分布列和数学期望
.
相关试题
－A)＋cos(π＋A)＝－
．
＋α)，求下列各式的值：
；
)(x≠0)，且cosα＝
x，求sinα、tanα的值．
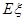的弧长；相关知识点
推荐套卷
（本小题满分12分）将编号为1，2，3，4的四张同样材质的卡片，随机放入编码分别为1，2，3，4的四个小盒中，每盒仅放一张卡片，若第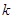号卡片恰好落入第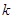号小盒中，则称其为一个匹对，用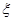表示匹对的个数.
（1）求第2号卡片恰好落入第2号小盒内的概率;
（2）求匹对数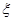的分布列和数学期望.
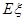粤公网安备 44130202000953号