（本题12分）已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，左视图（或称侧视图）是一个底边长为6、高为4的等腰三角形.
（1）求该几何体的体积V；
（2）求该几何体的侧面积S.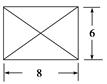
相关试题
.
的图象关于点
对称，直接写出
的值；
在区间
上恒成立，求
中，
，且
.
的面积；
，求
的长.
是首项为
，公差为
的等差数列，且
是等比数列
的前三项.
项和
.
.
的值；
的单调递增区间.推荐套卷
（本题12分）已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，左视图（或称侧视图）是一个底边长为6、高为4的等腰三角形.
（1）求该几何体的体积V；
（2）求该几何体的侧面积S.
粤公网安备 44130202000953号