两个完全相同的矩形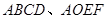
按如图所示的方式摆放，使点
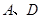均在
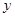轴的正半轴上，点B在第一象限，点
在
轴的正半轴上，点
在函数
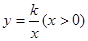的图象上
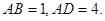
(1)求
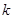的值．(2)将矩形
绕点B顺时针旋转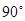
得到矩形
边
交函数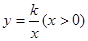的图象于点
求
的长．
，其中
，b=2。
。相关知识点
推荐套卷
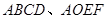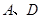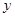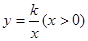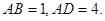
两个完全相同的矩形按如图所示的方式摆放，使点均在轴的正半轴上，点B在第一象限，点在轴的正半轴上，点在函数的图象上(1)求
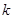的值．(2)将矩形
绕点B顺时针旋转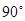得到矩形边交函数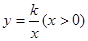的图象于点求的长．
粤公网安备 44130202000953号