..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知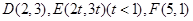 ,对任意
,对任意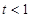 ,试判断
,试判断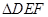 的形状;
的形状;
(Ⅱ)在平面内,已知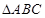 中,
中,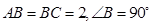 ,
,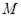 为
为 的中点,
的中点,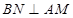 交
交 于
于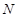 ,求证:
,求证: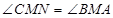 .
.
推荐套卷
..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知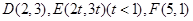 ,对任意
,对任意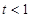 ,试判断
,试判断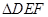 的形状;
的形状;
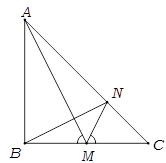
(Ⅱ)在平面内,已知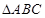 中,
中,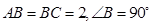 ,
,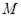 为
为 的中点,
的中点,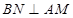 交
交 于
于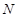 ,求证:
,求证: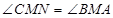 .
.