已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=2，任取a，b∈[﹣1，1]，a+b≠0，都有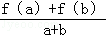
＞0成立．
（1）证明函数f（x）在[﹣1，1]上是单调增函数．
（2）解不等式f（x）＜f（x2）．
（3）若对任意x∈[﹣1，1]，函数f（x）≤2m2﹣2am+3对所有的a∈[0，
]恒成立，求m的取值范围．
相关试题
的终边的范围,并由此写出角
;(2)cos
.
是第二象限的角，试分别确定2
,
+
)=-
,且
(n∈Z).
+k
)=-2cos(
;
sin2
cos2
+cos
,
).求值：相关知识点
推荐套卷
已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=2，任取a，b∈[﹣1，1]，a+b≠0，都有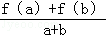＞0成立．
（1）证明函数f（x）在[﹣1，1]上是单调增函数．
（2）解不等式f（x）＜f（x2）．
（3）若对任意x∈[﹣1，1]，函数f（x）≤2m2﹣2am+3对所有的a∈[0，]恒成立，求m的取值范围．
粤公网安备 44130202000953号