(本小题满分12分)某公司为了实现2011年1000万元利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润昀25%,现有三个奖励模型: ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由.
(参考数据: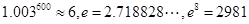 )
)
推荐套卷
(本小题满分12分)某公司为了实现2011年1000万元利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润昀25%,现有三个奖励模型: ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由.
(参考数据: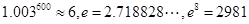 )
)