一种放射性元素，最初的质量为500g，按每年10﹪衰减．
（Ⅰ）求t年后，这种放射性元素质量ω的表达式；
（Ⅱ）由求出的函数表达式，求这种放射性元素的半衰期（剩留量为原来的一半所需要的时间）．（精确到0．1；参考数据：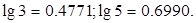
）
相关试题
=
，
、
为实数，
，
）处切线的斜率为
。
对任意的
，2）恒成立，求实数
的取值范围。
满足
，且
，图像在
轴上截得的线段长为
，求
的定义域为A,
(
<1) 的定义域为B.
A, 求实数
（2）
推荐套卷
一种放射性元素，最初的质量为500g，按每年10﹪衰减．
（Ⅰ）求t年后，这种放射性元素质量ω的表达式；
（Ⅱ）由求出的函数表达式，求这种放射性元素的半衰期（剩留量为原来的一半所需要的时间）．（精确到0．1；参考数据：）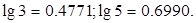
粤公网安备 44130202000953号