(本小题满分16分)平面直角坐标系xoy中,直线 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线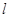 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线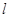 的方程;
的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。
相关知识点
推荐套卷
(本小题满分16分)平面直角坐标系xoy中,直线 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线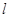 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线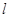 的方程;
的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。