（本小题满分14分）现有一张长为80cm，宽为60cm的长方形铁皮ABCD，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为100%，不考虑焊接处损失。如图，若长方形ABCD的一个角剪下一块铁皮，作为铁皮盒的底面，用余下材料剪拼后作为铁皮盒的侧面，设长方体的底面边长为x (cm),高为y (cm),体积为V （cm3）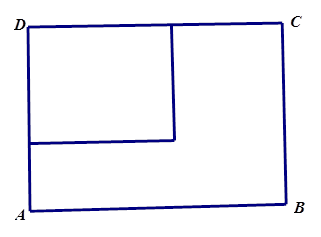
（1）求出x 与 y 的关系式；
（2）求该铁皮盒体积V的最大值；
相关试题
为锐角，
，求
的值．
>0为常数，若
上是增函数，求
若A
B恒成立，求实数
的取值范围．
，
，
．
，求角A的值．
．
的最小正周期；
时，求
中，角
所对的边分别为
，且
是方程
的两个根，且
，求：
的度数；（2）边
的长度．推荐套卷
（本小题满分14分）现有一张长为80cm，宽为60cm的长方形铁皮ABCD，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为100%，不考虑焊接处损失。如图，若长方形ABCD的一个角剪下一块铁皮，作为铁皮盒的底面，用余下材料剪拼后作为铁皮盒的侧面，设长方体的底面边长为x (cm),高为y (cm),体积为V （cm3）
（1）求出x 与 y 的关系式；
（2）求该铁皮盒体积V的最大值；
粤公网安备 44130202000953号