．某校为了解该校学生的课余活动情况，从阅读、运动、娱乐、其它四个方面
调查了若干名学生的爱好，经统计整理，绘制成不完整的扇形统计图与条形统计图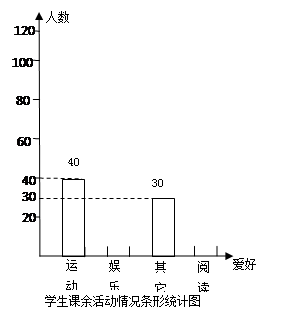
如下，请回答如下问题：
(1)本次共调查了多少人？
(2)把条形统计图补充完整；
(3)求其它所在扇形的圆心角的度数.
 |
和
．
坐标；
轴围成的三角形的面积；
，其中
，
.
在平面直角坐标系中的位置如图
的图象；
关于直线
，并写出
（
，
）是
的坐标为.
、
、
三点在同一条直线上，
，
，
．
相关知识点
推荐套卷
．某校为了解该校学生的课余活动情况，从阅读、运动、娱乐、其它四个方面
调查了若干名学生的爱好，经统计整理，绘制成不完整的扇形统计图与条形统计图如下，请回答如下问题：
(1)本次共调查了多少人？
(2)把条形统计图补充完整；
(3)求其它所在扇形的圆心角的度数.
|
粤公网安备 44130202000953号