(8分)(1)利用网格线画图: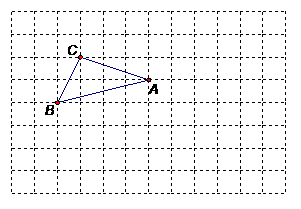
①过点A画AM⊥AC.
②将△ABC绕点A旋转180°,画出旋转后的图形.
(要在图中标出相关的点保留画图痕迹)
(2)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
注意:只需添加一个符合要求的正方形,并用阴影表示.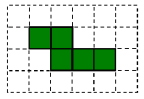
相关知识点
推荐套卷
(8分)(1)利用网格线画图:
①过点A画AM⊥AC.
②将△ABC绕点A旋转180°,画出旋转后的图形.
(要在图中标出相关的点保留画图痕迹)
(2)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
注意:只需添加一个符合要求的正方形,并用阴影表示.