.(12分)如图1：⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在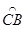
上取一点D，分别作直线CD、ED交直线AB于点F、M。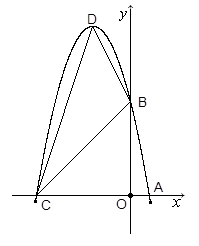
（1）求∠COA和∠FDM的度数；(3分)
（2）求证：△FDM∽△COM；(4分)
（3）如图2：若将垂足G改取为半径OB上任意一点，点D改取在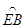
上，仍作直线CD、ED，分别交直线AB于点F、M，试判断：此时是否仍有△FDM∽△COM？证明你的结论。(5分)
，其中
是方程
的根．
，其中
．
+
）×
，然后选择一个你喜欢的数代入求值．
，其中a满足
．
，其中x=2．相关知识点
推荐套卷
.(12分)如图1：⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在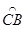上取一点D，分别作直线CD、ED交直线AB于点F、M。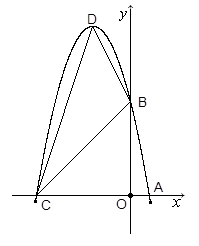
（1）求∠COA和∠FDM的度数；(3分)
（2）求证：△FDM∽△COM；(4分)
（3）如图2：若将垂足G改取为半径OB上任意一点，点D改取在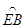上，仍作直线CD、ED，分别交直线AB于点F、M，试判断：此时是否仍有△FDM∽△COM？证明你的结论。(5分)
粤公网安备 44130202000953号