有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数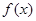 =
=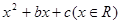 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数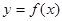 有零点的概率;
有零点的概率;
(Ⅱ) 求函数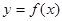 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率
推荐套卷
有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数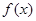 =
=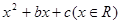 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数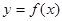 有零点的概率;
有零点的概率;
(Ⅱ) 求函数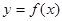 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率