（（本小题满分12分）设x，y∈R，
，
为直角坐标平面内x，y轴正方向上单位向量，若
向量
，
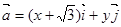，且
．
（1）求点M（x，y）的轨迹C的方程；
（2）若直线L与曲线C交于A、B两点，若
求证直线L与某个定圆E相切，并求出定圆E的方程。
相关试题
，判断并用单调性定义证明函数
，在
上的单调性．
，
．
的图象；
的解集．
（a＞0,b＞0）
；
的图象恒在函数
的图象的上方，求实数
的取值范围．
中，直线
的极坐标方程为
，
是
在射线
上，且满足
，记点
．
的距离的最大值．推荐套卷
（（本小题满分12分）设x，y∈R，，为直角坐标平面内x，y轴正方向上单位向量，若
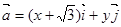向量，，且．
（1）求点M（x，y）的轨迹C的方程；
（2）若直线L与曲线C交于A、B两点，若求证直线L与某个定圆E相切，并求出定圆E的方程。
粤公网安备 44130202000953号