、如图，椭圆E经过点
，对称轴为坐标轴，焦点F1，F2在
轴上，离心率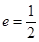
，
⑴求椭圆E的方程；
⑵求∠F1AF2的角平分线所在的直线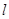
的方程；
⑶在椭圆E上是否存在关于直线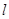对称的相异两点？若存在，请找出；若不存在，说明理由。
相关试题
对应的变换作用下得到直线m：x－y－4＝0，求实数a，b的值．
的特征值及对应的特征向量．
如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F.求证：
(1)∠AED＝∠AFD；
(2)AB2＝BE·BD－AE·AC.
，an＋1＝
(n∈N*)．推荐套卷
、如图，椭圆E经过点，对称轴为坐标轴，焦点F1，F2在轴上，离心率，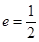
⑴求椭圆E的方程；
⑵求∠F1AF2的角平分线所在的直线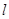的方程；
⑶在椭圆E上是否存在关于直线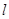对称的相异两点？若存在，请找出；若不存在，说明理由。
如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F.求证：
(1)∠AED＝∠AFD；
(2)AB2＝BE·BD－AE·AC.
粤公网安备 44130202000953号