（本小题满分12分）已知A（
，0），B（
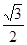，0）为平面内两定点，动点P满足|PA|+|PB|=2．
（I）求动点P的轨迹方程；
（II）设直线
与（I）中点P的轨迹交于M、N两点．求△BMN的最大面积及此时直线l的方程.
表示的平面区域，并求其面积．
过两点
和
，求
，
，
，如图所示，若直线
过
点且与线段
公共点，试求直线
的取值范围．
且和直线
垂直的直线的方程．
，点
，在第一象限的动点
满足
，求点
推荐套卷
（本小题满分12分）已知A（，0），B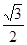（，0）为平面内两定点，动点P满足|PA|+|PB|=2．
（I）求动点P的轨迹方程；
（II）设直线与（I）中点P的轨迹交于M、N两点．求△BMN的最大面积及此时直线l的方程.
粤公网安备 44130202000953号