.若圆C过点M(0,1)且与直线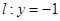 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点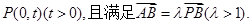
(I)求曲线E的方程; (II)若t=6,直线AB的斜率为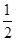 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
(III)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线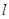 上,求证:t与
上,求证:t与 均为定值。
均为定值。
推荐套卷
.若圆C过点M(0,1)且与直线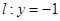 相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点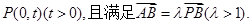
(I)求曲线E的方程; (II)若t=6,直线AB的斜率为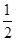 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
(III)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线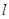 上,求证:t与
上,求证:t与 均为定值。
均为定值。