已知:如图,△ABC中,AB=3,∠BAC=120°,AC=1,D为AB延长线上一点,BD=1,点P在∠BAC的平分线上,且满足△PAD是等边三角形.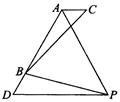
求证:BC=BP;
求点C到BP的距离.
相关知识点
推荐套卷
已知:如图,△ABC中,AB=3,∠BAC=120°,AC=1,D为AB延长线上一点,BD=1,点P在∠BAC的平分线上,且满足△PAD是等边三角形.
求证:BC=BP;
求点C到BP的距离.