如图1,已知,CE是Rt△ABC的斜边AB上的高,点P是CE的延长线上任意一点,BG⊥AP,
求证:(1)△AEP∽△DEB
(2) CE2=ED·EP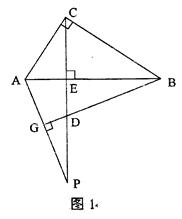
若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED·EP还成立吗?若成立,请给出证明;若不成立,请说明理由.(图2和图3挑选一张给予说明即可)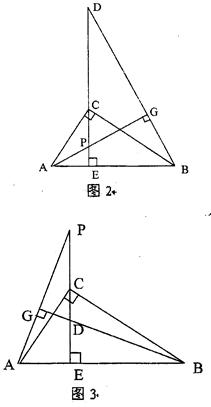
相关知识点
推荐套卷
如图1,已知,CE是Rt△ABC的斜边AB上的高,点P是CE的延长线上任意一点,BG⊥AP,
求证:(1)△AEP∽△DEB
(2) CE2=ED·EP
若点P在线段CE上或EC的延长线上时(如图2和图3),上述结论CE2=ED·EP还成立吗?若成立,请给出证明;若不成立,请说明理由.(图2和图3挑选一张给予说明即可)