(本小题10分)如图, 抛物线 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程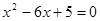 的两个实数根.
的两个实数根.
(1)求A、B两点的坐标;
(2) 求出此抛物线的的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
相关知识点
推荐套卷
(本小题10分)如图, 抛物线 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程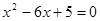 的两个实数根.
的两个实数根.
(1)求A、B两点的坐标;
(2) 求出此抛物线的的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.