（满分9分）如图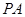
、
是半径为1的
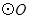的两条切线，点
、
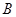分别为切点，
∠APB＝60°,OP与弦AB交于点C,与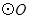交于点D.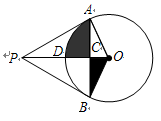
（1）在不添加任何辅助线的情况下，写出图中所有的全等三角形；
（2）求阴影部分的面积（结果保留
）．
相关试题
的值．
=2，则x2+
= _________ ，x3+
= _________ ，x4+
= _________ ．任意正整数n，猜想：
= _________ ．
，求a2b2与（a+b）4的值．
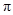×42012．相关知识点
推荐套卷
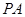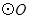（满分9分）如图、是半径为1的的两条切线，点、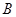分别为切点，
∠APB＝60°,OP与弦AB交于点C,与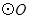交于点D.（1）在不添加任何辅助线的情况下，写出图中所有的全等三角形；
（2）求阴影部分的面积（结果保留
）．
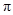粤公网安备 44130202000953号