如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.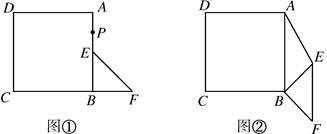
(1)若取AE的中点P,求证: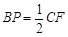 ;
;
(2)在图①中,若将△BEF绕点B顺时针方向旋转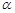 (
(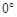 <
<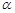 <
<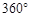 ),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角
),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角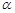 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由;
相关知识点
推荐套卷
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.
(1)若取AE的中点P,求证: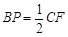 ;
;
(2)在图①中,若将△BEF绕点B顺时针方向旋转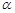 (
(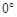 <
<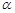 <
<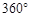 ),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角
),如图②,是否存在某位置,使得AE∥BF,若存在,求出所有可能的旋转角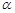 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由;