如图1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．求证：ME = MF．
如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．
如图3，若将原题中的“正方形”改为“矩形”，且AB = mBC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．
根据前面的探索和图4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由
相关试题
，其中
，
满足
．
数学思想运用：
（1）如图①所示，△ABC的外角平分线交于G，若∠A=80°，则∠BGC= °，请你猜测∠BGC和∠A的数量关系： ．
（2）如图②所示，若△ABC的内角平分线交于点I，若∠A=50°，则∠BIC= °，请你猜测∠BIC和∠A的数量关系： ．
（3）已知，如图③，△ABC中，
的平分线与
的平分线交于
点，请你猜测∠D和∠A的数量关系： ．
若
，求
的度数（写出求解过程）．
，
于点
，
于点E，
与
相交于点
．
；
，
，试判断直线
（1）求
的值。（2）求
的值。相关知识点
推荐套卷
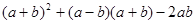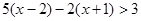
粤公网安备 44130202000953号