本题共有2个小题，第(1)小题满分5分，第(2)小题满分9分．
设双曲线
，
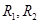是它实轴的两个端点，
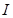是其虚轴的一个端点.已知其一条渐近线的一个方向向量是
，
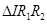的面积是
，
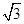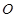为坐标原点，直线
与双曲线C相交于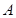
、
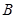两点，且
．
（1）求双曲线
的方程；
（2）求点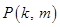
的轨迹方程,并指明是何种曲线.
相关试题
满足：
，
.
.
及
；
,
（
），求数列
的前
项和
.
中,BC=a,AC=b,a,b是方程
的两个根，且2COS(A+B)=1.
是首项是2，公比为q的等比数列，其中
是
与
的等差中项. 
.
项的和 
，求数列的通项公式.相关知识点
推荐套卷
本题共有2个小题，第(1)小题满分5分，第(2)小题满分9分．
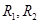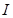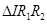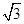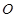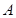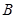设双曲线，是它实轴的两个端点，是其虚轴的一个端点.已知其一条渐近线的一个方向向量是，的面积是，为坐标原点，直线与双曲线C相交于、两点，且．
（1）求双曲线的方程；
（2）求点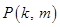的轨迹方程,并指明是何种曲线.
粤公网安备 44130202000953号