一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少?若把它看作是抛物线的一部分,在坐标系中(如图1)可设抛物线的表达式为
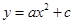 .
.
请你填空:a= ,c= ,EF= 米.若把它看作是圆的一部分,则可构造图形(如图2)计算如下:
设圆的半径是r米,在Rt△OCB中,易知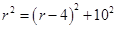 ,r=14.5
,r=14.5
同理,当水面上升3米至EF,在Rt△OGF中可计算出GF= 米,即水面宽度EF= 米.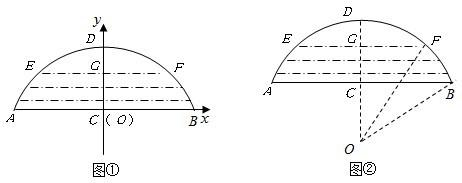
相关知识点
推荐套卷
 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).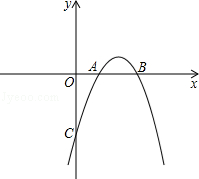

 .
.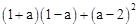 ,其中a=-3.
,其中a=-3. 粤公网安备 44130202000953号
粤公网安备 44130202000953号