(12分)如图7-15,在正三棱柱ABC—A1B1C1中,各棱长都等于a,D、E分别是AC1、BB1的中点,
(1)求证:DE是异面直线AC1与BB1的公垂线段,并求其长度;
(2)求二面角E—AC1—C的大小;
(3)求点C1到平面AEC的距离。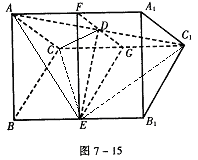
推荐套卷
(12分)如图7-15,在正三棱柱ABC—A1B1C1中,各棱长都等于a,D、E分别是AC1、BB1的中点,
(1)求证:DE是异面直线AC1与BB1的公垂线段,并求其长度;
(2)求二面角E—AC1—C的大小;
(3)求点C1到平面AEC的距离。