如图是某重点中学学校运动场平面图，运动场总面积15000平方米，运动场是由一个矩形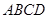
和分别以
、
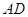为直径的两个半圆组成，塑胶跑道宽8米，已知塑胶跑道每平方米造价为150元，其它部分造价每平方米80元，
（Ⅰ）设半圆的半径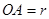
（米），写出塑胶跑道面积
与
的函数关系式
；
（Ⅱ）由于受运动场两侧看台限制，的范围为
，问当为何值时，运动场造价最低（第2问
取3近似计算）.
相关试题
的前
项和为
，
，
.
是等差数列. 
是数列
的前
项和，求使
对所有的
都成立的最大正整数
的值.
,又A∩B={x|x2+ax+b＜0},求a+b的值。
是满足不等式
≥
的自然数
的个数．
，求
；
，由（2）中
及
构成函数
，
，求推荐套卷
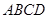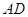如图是某重点中学学校运动场平面图，运动场总面积15000平方米，运动场是由一个矩形和分别以、为直径的两个半圆组成，塑胶跑道宽8米，已知塑胶跑道每平方米造价为150元，其它部分造价每平方米80元，
（Ⅰ）设半圆的半径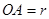（米），写出塑胶跑道面积与的函数关系式；
（Ⅱ）由于受运动场两侧看台限制，的范围为，问当为何值时，运动场造价最低（第2问取3近似计算）.
粤公网安备 44130202000953号